Paralaksą nazywamy zmianę położenia obiektu widzianego z dwóch rożnych punktów. Często położenie to rozpatruje się względem innych obiektów, znajdujących się w pewnej odległości za obiektem obserwowanym. Słowem paralaksa określa się zarówno samo zjawisko jak i wartość zmiany położenia tego obiektu. Ta zmiana położenia ciała na tle innych obiektów to jednocześnie zmiana kierunku obserwacji tego ciała o dany kąt.
Wyróżniamy następujące rodzaje paralaksy w astronomii:
* paralaksa dobowa (geocentryczna paralaksa równikowa), związana z ruchem obrotowym Ziemi,
* paralaksa geocentryczna południkowa, związana ze zmianą szerokości geograficznej obserwatora,
* paralaksa roczna (paralaksa heliocentryczna), związana z ruchem Ziemi po orbicie wokółsłonecznej.
Paralaksa jest zmianą pozycji obserwowanego obiektu astronomicznego spowodowaną przesunięciem się obserwatora. Obserwatorowi stojącemu na Ziemi wydaje się, że wszystkie gwiazdy są w tej samej odległości od Ziemi. Tymczasem, gwiazdy i inne obiekty astronomiczne znajdują się w bardzo różnych odległościach od nas, ale nasze oko jest tak zbudowane, że nie umiemy zauważyć tych różnic.
Paralaksa dobowa (geocentryczna paralaksa równikowa):
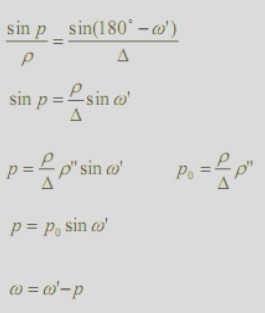
Paralaksa roczna (heliocentryczna) stała się podstawą definicji parseka, jednostki odległości używanej w astronomii. Parsek pc to odległość , z której 1 j.a. jest widoczna pod kątem 1" . Parsek jest czasem za mały na określenie odległości, więc astronomowie stosują jego wielokrotność: kiloparsek (kps) = tysiąc parseków i megaparsek (Mps) = milion parseków.
Jaki jest związek pomiędzy kątem paralaksy a odległością ?
Aby zrozumieć zależność kąta pomiędzy odległością wykonajmy samemu proste zadanie. Wybierzmy pewien obiekt w przestrzeni, który możemy określić jako słup, może to być oczywiście też ściana budynku lub drzewo. Wybrawszy obiekt (słup) zaznaczmy na nim dwa punkty A i B. Jak widać na rysunku, punkt A zaznaczamy powyżej punktu B. Gdyby słup miał około 3 m wysokości punkt B należy zaznaczyć na wysokości oczu, natomiast punkt A na wierzchołku. Mierzymy w cm odległość AB. Teraz wystarczy zmierzyć kąt β stojąc w punkcie C. Kąt β mierzymy jakąkolwiek ćwiartką okręgu z naniesioną podziałką kątową.
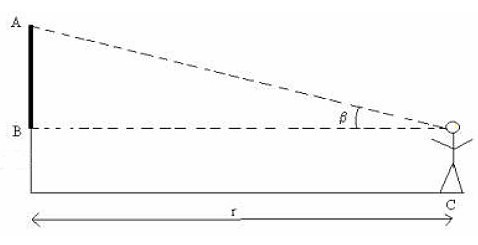
Rysunek. Samodzielny pomiar paralaksy
Gdy dokonujemy pomiarów z coraz większej odległości do słupa, kąt widzenia obiektu maleje, czyli większa odległość to mniejsza paralaksa. Posiadając dane wartości kąta oraz odległość punktów AB, możemy obliczyć odległość r od obiektu (słupa) do punktu pomiaru C:
tan β = AB / r
odległość r = AB / tan β
Kąt paralaksy maleje, gdy rośnie odległość do obiektu. Gdy obiekt jest bardzo odległy, kąt paralaksy jest bardzo mały.
W przypadku bardzo małych kątów można wartość tangensa kąta β zastąpić jego wartością w mierze łukowej (w radianach).
Starożytni greccy astronomowie wiedzieli o paralaksie. Jednakże nie mogli dostrzec rocznej paralaksy w pozycji gwiazd, dlatego wywnioskowali, że Ziemia nie może się obracać dookoła Słońca. Nie zdawali sobie jednak sprawy, że gwiazdy są miliony razy dalej niż Słońce, więc efekt paralaksy jest niemożliwy do zauważenia gołym okiem.
Opracowanie tekstu: Agnieszka Zawada


