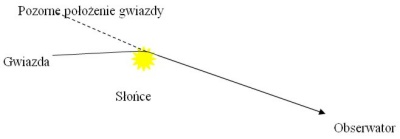
Geometria to dział matematyki zajmujący się badaniem figur geometrycznych i zależności między nimi. Istnieje wiele rodzajów geometrii, pierwsza i podstawowa jest euklidesowa. Geometria euklidesowa to dział geometrii oparty na określonym układzie pojęć pierwotnych i aksjomatów. Te aksjomaty przekazywane w edukacji traktujemy jako pewnik, z którym się nie dyskutuje. Aksjomat w języku greckim oznacza pewność, oczywistość.
Przykład aksjomatu. W każdym trójkącie suma miar kątów wewnętrznych wynosi 180o a + b + c = 180°
a1 + c + b1 = 180° a = a1 - kąt naprzemianległy ß = ß1 - kąt naprzemianległy
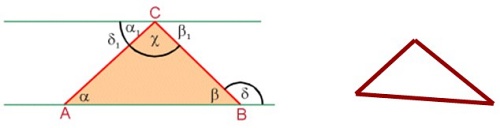
Linie równoległe nie przecinają się. Rysunek przedstawia przestrzeń euklidesową. Trójkąt i linie równoległe.

W geometrii wszechświata sumy kątów jednak mogą być większe lub mniejsze niż 180o . W kosmosie nie można stosować tylko aksjomatów geometrii euklidesowej. Przykładem geometrii nieeuklidesowej jest geometria Riemanna. Geometria Riemanna to geometria sferyczna, tyle że w trzech wymiarach. Aby ją stworzyć, niemiecki matematyk musiał nie tylko odrzucić postulat Euklidesa, ale również pierwszy pewnik, który brzmi: Przez dwa punkty można przeprowadzić tylko jedną prostą. Trójkąt i linie w geometrii nieeuklidesowej. Geometria Riemanna: powierzchnia kuli, krzywizna dodatnia. Suma kątów w trójkącie jest większa niż 1800 . Linie równoległe przecinają się (przykład: południki).

Trójkąt i linie w geometrii nieeuklidesowej. Geometria Riemanna: powierzchnia siodłowa, krzywizna ujemna. Suma kątów w trójkącie jest mniejsza niż 1800 . Linie równoległe rozchodzą się.